Расчёт передаточного отношения редуктора - правильный метод

Статья обновлена: 04.08.2025

Передаточное отношение редуктора – ключевая характеристика, определяющая его влияние на крутящий момент и скорость вращения выходного вала. От правильного расчёта этого параметра напрямую зависит эффективность и долговечность всей механической системы.

В статье рассмотрены основные методы расчёта передаточного отношения для разных типов редукторов: цилиндрических, червячных, планетарных и комбинированных. Вы научитесь определять соотношение с помощью количества зубьев шестерён, диаметров шкивов или угловых скоростей, избегая распространённых ошибок.

Суть передаточного отношения в механике

Передаточное отношение редуктора (i) – это фундаментальная характеристика, количественно описывающая преобразование параметров вращательного движения между входным и выходным валами механизма. Физически оно выражает, во сколько раз изменяются угловая скорость и крутящий момент при передаче усилия через систему взаимодействующих зубчатых колес или других элементов.

Ключевая суть передаточного отношения заключается в законе сохранения энергии (без учета потерь на трение). Мощность на входе (P₁) теоретически равна мощности на выходе (P₂). Учитывая, что P = Mω (где M – момент силы, ω – угловая скорость), равенство M₁ω₁ ≈ M₂ω₂ приводит к обратной зависимости между моментом и скоростью: увеличение одного параметра неизбежно вызывает уменьшение другого. Именно передаточное отношение определяет масштаб этого преобразования.

Основные аспекты передаточного отношения:

Формула расчета: i = ω₁ / ω₂ = n₁ / n₂ = d₂ / d₁ = z₂ / z₁

где:

ω₁, n₁ – угловая скорость и частота вращения входного (ведущего) вала,
ω₂, n₂ – угловая скорость и частота вращения выходного (ведомого) вала,
d₁, z₁ – диаметр делительной окружности и число зубьев ведущей шестерни,
d₂, z₂ – диаметр делительной окружности и число зубьев ведомой шестерни.

Типы передаточных отношений:

i > 1 (Например, i=3:1)	Понижающая передача	Уменьшает скорость (n₂ < n₁), увеличивает крутящий момент (M₂ > M₁). Основное назначение редукторов.
i < 1 (Например, i=1:2)	Повышающая передача	Увеличивает скорость (n₂ > n₁), уменьшает крутящий момент (M₂ < M₁). Встречается реже, например, в мультипликаторах.

Важное следствие: i косвенно определяет необходимое усилие и скорость выполнения работы на выходном валу. Правильный расчет i позволяет точно подобрать редуктор, обеспечивающий требуемые рабочие характеристики исполнительного механизма.

Ведущий и ведомый вал: ключевая терминология

При расчете передаточного отношения редуктора необходимо четко различать понятия ведущего и ведомого вала. Ведущий вал (его также называют входным или первичным валом) получает вращательное движение непосредственно от привода – например, электродвигателя или ДВС. Именно он передает крутящий момент на элементы редукторного механизма.

Ведомый вал, в свою очередь, именуется выходным или вторичным. Он получает преобразованное в редукторе вращение и передает его рабочему оборудованию – конвейеру, насосу или другому механизму. Главная задача редуктора – изменить характеристики крутящего момента и угловой скорости, выдаваемые ведомым валом, относительно параметров ведущего.

Критичные принципы для корректного расчета:

Ведущий вал вращается с исходной скоростью (n_вх), а ведомый – с результирующей (n_вых)
Зубчатые зацепления внутри редуктора связывают эти два вала, изменяя параметры вращения
Диаметры шестерен (d) или количества зубьев (z) на валах прямо влияют на передаточное число

Расчетные соотношения:

Параметр	Формула	Пояснение
Передаточное отношение (i)	i = n_вх / n_вых	Отношение скоростей ведущего/ведомого валов
Через зубья шестерен	i = z_{ведомый} / z_{ведущий}	Отношение зубьев ведомой шестерни к ведущей
Через диаметры колес	i = d_{ведомый} / d_{ведущий}	Отношение диаметров ведомой/ведущей шестерен

Важно: При каскадных редукторах общее передаточное отношение определяется перемножением отношений каждой ступени (i_общ = i₁ × i₂ × ... × i_n). Ошибка в идентификации ведущих и ведомых элементов на любой ступени ведет к неверным результатам.

Базовая формула для расчета передаточного числа

Передаточное отношение (i) определяется как соотношение угловых скоростей входного и выходного валов редуктора. Оно также равно отношению числа зубьев ведомой шестерни к числу зубьев ведущей шестерни в зубчатой передаче. Эта величина показывает степень преобразования крутящего момента и скорости вращения.

Для одной ступени редуктора используйте формулу:

i = Z₂ / Z₁

где Z₂ – количество зубьев ведомой шестерни, Z₁ – количество зубьев ведущей шестерни. В многоступенчатых редукторах общее передаточное отношение равно произведению отношений всех ступеней: i_общ = i₁ × i₂ × ... × i_n.

Связь количества зубьев шестерен с передаточным отношением

Количество зубьев напрямую определяет передаточное отношение (i) в зубчатой передаче. Для пары цилиндрических шестерен это отношение равно частному от деления числа зубьев ведомой шестерни (Z_вед) на число зубьев ведущей шестерни (Z_ведщ). Формула расчета приобретает вид: i = Z_вед / Z_ведщ. Например, если ведущая шестерня имеет 20 зубьев, а ведомая – 60, передаточное отношение будет i = 60 / 20 = 3.

Значение i определяет преобразование параметров вращения. При i > 1 (когда Z_вед > Z_ведщ) происходит снижение частоты вращения и увеличение крутящего момента на выходе (понижающая передача). И наоборот: при i < 1 (Z_вед < Z_ведщ) частота вращения растет, а крутящий момент падает (повышающая передача). Параллельно изменяется направление вращения: внешнее зацепление шестерен инвертирует его, внутреннее – сохраняет.

Особенности расчета для многоступенчатых редукторов

Если редуктор включает несколько последовательных передач, общее передаточное отношение (i_общ) равно произведению передаточных отношений всех ступеней:

i_общ = i₁ × i₂ × ... × i_n
Каждое i_k рассчитывается для своей пары: i_k = Z_{вед k} / Z_{ведщ k}.

Пример расчета: Двухступенчатый редуктор:

Первая ступень: Z_ведщ1 = 30, Z_вед1 = 90 → i₁ = 90 / 30 = 3
Вторая ступень: Z_ведщ2 = 25, Z_вед2 = 100 → i₂ = 100 / 25 = 4
Итог: i_общ = 3 × 4 = 12

Тип передачи	Соотношение зубьев	Передаточное отношение	Эффект
Понижающая	Z_вед > Z_ведщ	i > 1	↑ Момент, ↓ Скорость
Повышающая	Z_вед < Z_ведщ	i < 1	↓ Момент, ↑ Скорость

Погрешности расчета зубьев (деформации, зазоры) и КПД передачи могут незначительно корректировать реальное значение i. Для проектирования критичных систем используйте запас прочности и учитывайте механические потери.

Расчет передаточного отношения для пар цилиндрических прямозубых шестерен

Основная формула для одиночной пары цилиндрических прямозубых шестерен: i = z₂ / z₁, где z₂ – число зубьев ведомой шестерни, z₁ – ведущей. Например, при z₁=20 зубьев на ведущем валу и z₂=60 на ведомом: i = 60/20 = 3. Это означает трёхкратное увеличение крутящего момента и пропорциональное снижение частоты вращения.

Для многоступенчатого редуктора с последовательным зацеплением пар общее передаточное отношение определяется произведением отношений каждой ступени: i_общ = i₁ × i₂ × ... × i_n. Приведенный порядок сохраняет последовательность: считаем от входного вала первой ступени к выходному валу последующей.

Практические аспекты расчета

Диаметры шестерен: Ориентируйтесь на делительные диаметры d (мм). Отношение d₂/d₁ также даст передаточное число при отсутствии данных о зубьях.
Частота вращения: Альтернативная формула: i = n₁ / n₂, где n₁ – обороты ведущего вала (об/мин), n₂ – ведомого.
Межосевое расстояние: Рассчитывается как a_w = (d₁ + d₂)/2 = m(z₁ + z₂)/2, где m – модуль зацепления (мм).

Параметр	Ведущая шестерня	Ведомая шестерня
Число зубьев (z)	z₁	z₂
Диаметр (d)	d₁ = m × z₁	d₂ = m × z₂
Частота вращения (n)	n₁	n₂ = n₁ / i

Определите параметры ведущей шестерни (z₁ или d₁).
Измерьте/выберите z₂ ведомой шестерни.
Вычислите i по формуле i = z₂ / z₁.
Для проверки: убедитесь, что n₂ = n₁ / i и d₂ = d₁ × i.

Определение передаточного отношения по диаметрам шкивов

Для ременных и цепных передач передаточное отношение (i) напрямую определяется соотношением диаметров шкивов при условии отсутствия проскальзывания.

Формула расчета в одномашинной передаче проста и основана на зависимости линейных скоростей точек на поверхностях шкивов, которые должны быть равны.

Расчет передаточного отношения

Передаточное отношение (i) определяется как отношение диаметра ведомого шкива (D_ведом) к диаметру ведущего шкива (D_ведущ):

Формула: i = D_ведом / D_ведущ

Пояснения:

Ведомый шкив: Шкив, на который передается вращение от ведущего шкива через ремень или цепь.
Ведущий шкив: Шкив, получающий вращательное движение непосредственно от вала двигателя (или предыдущей ступени).
Если редуктор имеет несколько ступеней (например, последовательных пар шкивов), общее передаточное отношение (i_общ) рассчитывается как произведение передаточных отношений всех ступеней: i_общ = i₁ * i₂ * ... * i_n.

Таблица примеров:

D_ведущ (мм)	D_ведом (мм)	i = D_ведом / D_ведущ	Эффект
100	200	200 / 100 = 2.0	Снижение скорости в 2 раза, увеличение момента.
150	75	75 / 150 = 0.5	Увеличение скорости в 2 раза, снижение момента.
120	120	120 / 120 = 1.0	Скорость и момент не изменяются (передача прямая).

Помните:

Это отношение определяет, во сколько раз изменяется частота вращения валов: n_ведом = n_ведущ / i.
Данная формула актуальна только для передач, использующих шкивы одинакового (или пренебрежимо схожего) типа с общей линией контакта (ремень/цепь).

Особенности расчета для конических передач

Рассчет передаточного отношения (u) для конической передачи выполняется по той же базовой формуле, что и для цилиндрической: u = z₂ / z₁, где z₂ – число зубьев ведомого колеса (большего), а z₁ – число зубьев ведущего колеса (меньшего). Однако ключевое отличие заключается в учете взаимной геометрии конусов колес при определении кинематики усилий. Оси валов пересекаются под углом (чаще всего 90°), а зубья имеют переменный профиль по длине, что требует введения специфических параметров.

Основные особенности проектирования включают:

Углы конусов: Для ортогональных передач (сумма углов 90°) угол делительного конуса шестерни (δ₁) и колеса (δ₂) определяются как:
- δ₁ = arctan(1/u)
- δ₂ = 90° – δ₁
Эквивалентные числа зубьев: Для прочностных расчетов используют эквивалентное число зубьев (z_v), учитывающее угол конуса и наклон зуба:
- Прямозубая передача: z_v = z / cosδ
- Спиральная передача: z_v = z / (cosδ ⋅ cos³β)
где β – угол наклона зубьев.
Конусное расстояние (R_e): Рассчитывается через внешний делительный диаметр (d_e) и угол конуса: R_e = d_e / (2⋅sinδ).

Наиболее важные формулы для проектирования конической передачи:

Параметр	Формула
Передаточное отношение	u = z₂ / z₁ = ω₁ / ω₂
Внешний делительный диаметр (шестерни)	d_e1 = m_e ⋅ z₁
Угол конуса шестерни (Σ=90°)	δ₁ = arctan(1/u)
Конусное расстояние	R_e = d_e1 / (2⋅sinδ₁)
Средний окружной модуль	m_m = m_e ⋅ (1 - 0.5⋅b/R_e)

Примечание: Расчеты прочности зубьев (на контактные напряжения и изгиб) используют m_m и z_v для преобразования конической пары в эквивалентную цилиндрическую косозубую передачу. Это позволяет применять методики ГОСТ или ISO с поправкой на неравномерность нагрузки вдоль зуба.

Методика для червячных передач

Расчёт передаточного отношения (u) червячного редуктора базируется на соотношении числа зубьев ведомого червячного колеса (z₂) к числу заходов ведущего червяка (z₁). Формула имеет строго определённый вид и не зависит от модуля или межосевого расстояния. Данная зависимость объясняется принципом зацепления: за один оборот червяк смещает зубчатое колесо на количество зубьев, равное числу своих заходов.

Точное определение параметров z₁ и z₂ является критическим этапом. Число заходов червяка (z₁, обычно 1–4) определяют визуально – подсчётом витков резьбы на торцевой части. Число зубьев колеса (z₂, как правило >30 во избежание подреза) берут из паспорта изделия либо измеряют непосредственным подсчётом. Трение и КПД в расчёте u не учитываются – это чисто кинематический параметр.

Последовательность действий

Идентифицировать червяк: визуально определите число заходов резьбы z₁ (чаще всего – однозаходный или двухзаходный).
Идентифицировать колесо: подсчитайте полное количество зубьев z₂ на червячной шестерне.
Применить формулу: Рассчитайте передаточное отношение по уравнению:
u = z₂ / z₁

Практический пример

Компонент	Параметр	Значение	Пояснение
Червяк	Число заходов (z₁)	2	Двухзаходная резьба
Колесо	Число зубьев (z₂)	60	Стандартное исполнение
Передаточное отношение (u)		60 / 2 = 30	Редуктор понижает частоту вращения в 30 раз

Важное следствие: Однозаходные червяки (z₁=1) обеспечивают максимальное передаточное отношение для заданного размера колеса. Увеличение числа заходов червяка снижает u при неизменном z₂, что позволяет регулировать кинематику без изменения габаритов редуктора.

Примечание: Приведённая методика справедлива только для классических эвольвентных или архимедовых червячных пар. Специальные профили (конволютные, нелинейные) требуют уточнения в технической документации.

Передаточное отношение цепной передачи на практике

Расчет передаточного отношения (i) цепной передачи аналогичен другим зубчатым механизмам и определяется как отношение числа зубьев ведомой звездочки (Z₂) к числу зубьев ведущей звездочки (Z₁). Формула выражается как: i = Z₂ / Z₁. Например, при ведущей звездочке на 20 зубьев и ведомой на 60 зубьев передаточное отношение составит i = 60 / 20 = 3. Это означает, что ведомый вал вращается в 3 раза медленнее ведущего вала при одновременном увеличении крутящего момента.

Для корректного подбора компонентов необходимо учитывать не только передаточное отношение, но и межосевое расстояние между звездочками, нагрузку на цепь, тип цепи (роликовая, зубчатая) и условия эксплуатации. Ошибка в расчете может привести к проскальзыванию цепи, ускоренному износу зубьев или обрыву. Критично соблюдать допустимые минимальные и максимальные значения зубьев звездочек для конкретного типа цепи.

Ключевые аспекты для практической реализации

Проверка скорости цепи: Скорость цепи (V, м/с) вычисляется по формуле: **V = π * D * n / 60000, где D – диаметр делительной окружности звездочки (мм), n – частота вращения (об/мин). Значение не должно превышать пределов, указанных в таблицах для выбранного типа цепи.
Контроль шага цепи (P): Шаг цепи должен строго соответствовать шагу звездочек. Недопустима установка цепи с шагом, отличным от паспортного значения звездочки.
Фактор безопасности: При высоких нагрузках или ударных воздействиях вводят коэффициент запаса прочности (k). Требуемое передаточное отношение следует сопоставлять с реальным: iₚ = n₁ / n₂**, где n₁ и n₂ – фактические обороты ведущего/ведомого валов.

Пример расчета для электродвигателя: При Z₁=15, Z₂=45, i=45/15=3. Если двигатель вращается со скоростью 1800 об/мин, ведомая звездочка будет иметь: n₂=1800/3=600 об/мин.

Ременные передачи: тонкости вычислений

Расчет передаточного отношения (u) ременной передачи принципиально отличается от расчета для зубчатых передач из-за явления упругого скольжения ремня. В идеализированном случае без учета скольжения передаточное отношение определяется как отношение диаметров (или радиусов) ведущего (d1) и ведомого (d2) шкивов: u = n1 / n2 = d2 / d1 = D2 / D1, где n1 и n2 - частоты вращения ведущего и ведомого валов соответственно. Это соотношение известно как диаметральное передаточное отношение.

Однако на практике ремень под нагрузкой неизбежно проскальзывает относительно шкивов. Это приводит к тому, что фактическая скорость ведомого шкива (v2) меньше теоретической скорости (v2_theor), рассчитанной по диаметральному отношению. Скорость ремня (v) определяется скоростью ведущего шкива: v = π * d1 * n1. Теоретическая скорость ведомого шкива: v2_theor = π * d2 * n2_theor = v. Фактическая скорость ведомого шкива: v2 = π * d2 * n2. Из-за проскальзывания n2 < n2_theor и v2 < v2_theor.

Учет проскальзывания

Проскальзывание (ξ) количественно выражается как относительная потеря скорости:

Коэффициент проскальзывания: ξ = (v - v2) / v = (n2_theor - n2) / n2_theor
Фактическое передаточное отношение: u_real = n1 / n2 = (d2 / d1) / (1 - ξ)

Величина коэффициента проскальзывания ξ зависит от нескольких факторов:

Материал и тип ремня: Поликлиновые, зубчатые, плоские, клиновые ремни имеют разные характеристики скольжения.
Натяжение ремня: Недостаточное натяжение усиливает проскальзывание.
Нагрузка на валу (Крутящий момент): Чем выше нагрузка, тем больше скольжение.
Угол охвата ремнем шкивов: Меньший угол охвата (особенно на малом шкиве) увеличивает вероятность проскальзывания.

Типичные значения коэффициента проскальзывания ξ для предварительных расчетов:

Тип передачи	Коэффициент проскальзывания ξ (%)
Плоские ремни (кожаные, прорезиненные)	1 ... 2
Клиновые ремни	0.5 ... 1
Поликлиновые ремни	0.5 ... 1
Зубчатые ремни	0.1 ... 0.3 (скольжение практически отсутствует)

Важно помнить, что расчет по формуле u_real = d2 / (d1 * (1 - ξ)) дает номинальное значение. Реальное передаточное отношение в работающей передаче будет также зависеть от точности изготовления шкивов, температурных условий и состояния ремня.

Для открытых передач (ведущий и ведомый шкивы вращаются в одном направлении) расчет ведется по приведенным выше формулам. В случае перекрестной ременной передачи (шкивы вращаются в противоположных направлениях) угол охвата увеличивается, но возникает дополнительный изгиб ремня, что может влиять на его долговечность и требуемое натяжение.

При проектировании многоступенчатых редукторов с ременными передачами на разных ступенях общее передаточное отношение рассчитывается как произведение передаточных отношений отдельных ступеней: u_total = u1 * u2 * ... * un. Необходимо учитывать проскальзывание на каждой ступени для точного определения итоговой скорости выходного вала.

Планетарный редуктор: специфика расчета

Расчёт передаточного отношения (i) планетарных редукторов сложнее, чем у классических зубчатых передач, из-за подвижности элементов и возможности фиксации разных звеньев. Ключевая особенность – наличие вращающихся сателлитов, объединенных водилом, и взаимодействующих с центральными колесами (солнечным и корончатым).

Основу расчёта составляет метод Виллиса, рассматривающий относительное движение звеньев: i^аб = (ω_a - ω_в) / (ω_b - ω_в), где ω_a, ω_b, ω_в – угловые скорости солнечного колеса, корончатого колеса и водила соответственно. Знаменатель формулы соответствует статической передаче при условно остановленном водиле.

Алгоритм расчёта передаточного отношения:

Определить ведущее, ведомое звено и зафиксированный элемент.
Записать формулу Виллиса для пары с фиксированным водилом (для условного прямозубого зацепления):
- i^{сол-корон} = z_корон / z_сол, где z – числа зубьев.
Подставить известные скорости (нулевая для фиксированного звена) в формулу Виллиса и решить уравнение относительно выходной скорости.

Распространённые схемы и формулы i (ведущее → ведомое):

Фиксировано:	Формула передаточного отношения (i)
Корончатое колесо (ω_b = 0)	i = 1 + (z_корон / z_сол)
Солнечное колесо (ω_a = 0)	i = 1 + (z_сол / z_корон)
Водило (ω_в = 0)	i = - (z_корон / z_сол)

Знак минус в последнем случае указывает на смену направления вращения. Важность согласования чисел зубьев (обеспечение соосности, отсутствие интерференции) требует отдельного проектировочного расчёта геометрии передачи.

Многоступенчатые редукторы: принципы вычисления

Многоступенчатые редукторы объединяют несколько последовательных пар зубчатых колёс (или других передач), что позволяет достичь высоких общих передаточных отношений при рациональном распределении нагрузки между ступенями. Конструкция таких редукторов оптимизирует габариты, снижает инерционность системы и улучшает КПД за счёт уменьшения нагрузки на отдельные элементы.

Общее передаточное отношение \(u_{общ}\) многоступенчатого редуктора рассчитывается как произведение передаточных отношений всех его ступеней. Формула для \(n\) ступеней выглядит следующим образом: \[u_{общ} = u_1 \times u_2 \times u_3 \times \ldots \times u_n\] где \(u_1, u_2, \ldots, u_n\) – передаточные отношения каждой отдельной ступени.

Ключевые аспекты расчёта

Распределение передаточных отношений по ступеням требует соблюдения баланса:

Оптимальное соотношение: Передаточное отношение одной ступени обычно не превышает 6-7 для цилиндрических передач (до 10 для червячных) во избежание перегрузки.
Учёт КПД: Общий КПД редуктора (\(\eta_{общ}\)) равен произведению КПД всех ступеней: \[\eta_{общ} = \eta_1 \times \eta_2 \times \ldots \times \eta_n\]
Ограничения проектирования:
- Минимальный диаметр ведомого колеса ≥ 1.1 модуля × число зубьев
- Максимально допустимые окружные скорости для выбранного типа передачи
- Равенство межосевых расстояний в соосных ступенях

Пример расчёта трёхступенчатого редуктора:

Требуется \(u_{общ} = 80\). Варианты распределения:

• Равномерное: \(u_1=4.3\), \(u_2=4.3\), \(u_3=4.3\) → \(4.3^3 ≈ 80\)

• С замедлением: \(u_1=5.0\), \(u_2=4.0\), \(u_3=4.0\) → \(5×4×4=80\)

Важно: Расчёт ведётся от входного вала к выходному. Для редукторов с параллельными валами направления вращения ступеней чередуются.

Перемножение передаточных чисел на разных ступенях

Многоступенчатые редукторы содержат несколько последовательных пар зацепляющихся элементов (шестерён, червяков, зубчатых колёс). Каждая такая пара образует отдельную ступень преобразования вращения. Для корректной работы системы требуется определить итоговое передаточное отношение всего механизма.

Суммарный коэффициент передачи рассчитывается по формуле: i_общ = i₁ × i₂ × ... × i_n, где i₁, i₂, ..., i_n – передаточные числа отдельных ступеней. Последовательность перемножения соответвует расположению ступеней от входного вала к выходному.

Пример расчёта для трёхступенчатого редуктора

Каждая ступень имеет передаточные отношения:

Первая ступень (зубчатая пара): i₁ = 4
Вторая ступень (червячная передача): i₂ = 20
Третья ступень (косозубая передача): i₃ = 3

Общее передаточное отношение:

i_общ = 4 × 20 × 3 = 240

Элемент	Передаточное число
Ступень 1 (зубчатая)	4
Ступень 2 (червячная)	20
Ступень 3 (косозубая)	3
Итог	240

Примечания:

Если редуктор включает повышающие и понижающие ступени (i < 1 или i > 1), их значения перемножаются аналогично.
Для параллельных или разветвлённых кинематических цепей используются другие методы расчёта, включая векторное сложение.

Расчет общего передаточного отношения многоступенчатой системы

В многоступенчатом редукторе общее передаточное отношение (u_общ) определяется последовательным умножением передаточных отношений всех его ступеней. Каждая ступень, будь то цилиндрическая, коническая, червячная или планетарная передача, вносит свой множитель в общий коэффициент преобразования скорости и крутящего момента. Этот подход применим независимо от типа используемых передач и их комбинации.

Формула для расчета выглядит следующим образом: u_общ = u₁ × u₂ × u₃ × ... × u_n, где u₁, u₂, ..., u_n – передаточные отношения отдельных ступеней. Важно корректно определять направление вращения: если передача меняет его (например, червячная или нечетное число внешних зацеплений), это учитывается знаком минус в промежуточных расчетах.

Ключевые аспекты расчета

Идентификация ступеней: Четко выделите все механические пары в кинематической цепи, где происходит преобразование частоты вращения.
Последовательное перемножение: Умножайте значения u строго по порядку прохождения потока мощности от входного вала к выходному.
Учет направления вращения: Для реверсивных передач (червячные, гипоидные) используйте отрицательные значения u при определении итогового знака.
Проверка диапазонов: Убедитесь, что для каждой ступени полученные частоты вращения и моменты соответствуют техническим ограничениям материалов и конструкций.

Пример расчета для двухступенчатого редуктора

Ступень	Тип передачи	Передаточное отношение (u)
1 (Входная)	Цилиндрическая (z₁=20, z₂=60)	u₁ = z₂/z₁ = 60/20 = 3.0
2 (Выходная)	Червячная (z_ч=2, z_к=40)	u₂ = z_к/z_ч = 40/2 = 20.0
Общее	–	u_общ = u₁×u₂ = 3.0×20.0 = 60.0

Влияние передаточного отношения на выходную скорость

Передаточное отношение редуктора (i) напрямую определяет изменение выходной скорости вращения относительно входной. Это отношение выражается формулой: i = ω_вх / ω_вых, где ω_вх – угловая скорость входного вала, а ω_вых – угловая скорость выходного вала. Таким образом, выходная скорость всегда обратно пропорциональна передаточному числу.

Чем выше передаточное отношение редуктора, тем значительнее снижается выходная скорость. Например, при i=5:1 входной вал, вращающийся со скоростью 1500 об/мин, обеспечит выходную скорость только 300 об/мин. И наоборот, редукторы с меньшими значениями (например, i=2:1) демонстрируют меньшую потерю скорости на выходном валу.

Ключевые закономерности

Прямая зависимость: Выходная скорость рассчитывается как: ω_вых = ω_вх / i.
Ограничения: Чрезмерно высокое i может приводить к нежелательному падению скорости ниже эксплуатационных требований.
Компромисс с моментом: Снижение скорости увеличивает выходной крутящий момент по формуле M_вых = M_вх × i × η (где η – КПД редуктора).
Системные последствия: Выбор неподходящего i вызывает перегрузки или недостаточную производительность механизма.

Для наглядности рассмотрим типовые сценарии:

Высокое i (10:1) при ω_вх = 1800 об/мин → ω_вых = 180 об/мин (высокий момент, низкая скорость).
Низкое i (1.5:1) при ω_вх = 1800 об/мин → ω_вых = 1200 об/мин (умеренный момент, высокая скорость).

Передаточное отношение (i)	Входная скорость (об/мин)	Выходная скорость (об/мин)	Эффект
10:1	1500	150	Резкое снижение скорости
3:1	1500	500	Умеренное снижение

Взаимосвязь передаточного числа и крутящего момента

Крутящий момент на выходном валу редуктора напрямую зависит от передаточного отношения: чем выше передаточное число, тем больше усилие преобразуется механизмом. Эта зависимость описывается формулой:
М_вых = М_вх × i × η,
где М_вх – входной момент, i – передаточное число, а η – КПД редуктора.

Обратная зависимость наблюдается для скорости вращения: выходные обороты уменьшаются пропорционально увеличению передаточного числа. Математически:
n_вых = n_вх / i,
где n_вх – входная частота вращения, n_вых – выходная.

Ключевые аспекты взаимного влияния

При выборе передаточного отношения учтите следующие закономерности:

Прямая пропорциональность момента: Увеличение i в 3 раза даёт ≈3-кратный рост выходного момента (с поправкой на потери КПД).
Границы эффективности: Сверхвысокие значения i (например, >100) снижают КПД из-за роста потерь на трение и инерции.
Баланс характеристик: Рост момента приводит к пропорциональному снижению скорости – нельзя одновременно достичь максимума обоих параметров.

Передаточное число (i)	Выходной момент (относительно входа)	Выходная скорость (относительно входа)
1:1	≈1× (без изменения)	100%
5:1	≈5×	20%
10:1	≈10×	10%

Примечание: Реальные значения момента всегда меньше расчётных из-за потерь КПД (обычно 85-98% для 1 ступени). Многоступенчатые редукторы умножают КПД каждой ступени.

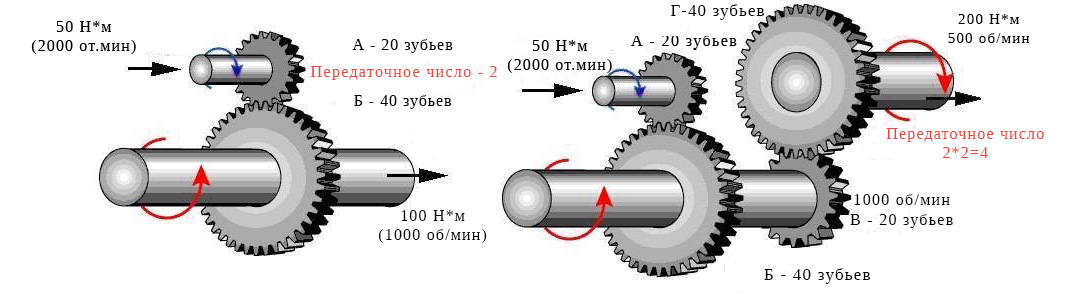
Пример расчета для двухступенчатого цилиндрического редуктора

Рассмотрим двухступенчатый цилиндрический редуктор, где каждая ступень имеет собственное передаточное отношение. Общее передаточное отношение (i_общ) определяется как произведение передаточных отношений первой (i₁) и второй (i₂) ступеней: i_общ = i₁ × i₂. Исходные параметры: ведущая шестерня первой ступени с числом зубьев z₁ = 20 вращает ведомую шестерню z₂ = 80; ведущая шестерня второй ступени z₃ = 25 взаимодействует с ведомой шестерней z₄ = 100.

Для расчета первой ступени используем формулу i₁ = z₂ / z₁ = 80 / 20 = 4. Для второй ступени: i₂ = z₄ / z₃ = 100 / 25 = 4. Общее передаточное отношение: i_общ = i₁ × i₂ = 4 × 4 = 16. Данные удобно свести в таблицу:

Ступень	Ведущая шестерня (зубья)	Ведомая шестерня (зубья)	Передаточное отношение
Первая	z₁ = 20	z₂ = 80	i₁ = 80 / 20 = 4
Вторая	z₃ = 25	z₄ = 100	i₂ = 100 / 25 = 4
Итого	i_общ = 4 × 4 = 16

Расчет по оборотам входного и выходного валов

Для расчета передаточного отношения редуктора через количество оборотов валов используется прямой экспериментальный метод. Замерьте количество оборотов входного и выходного валов за одинаковый промежуток времени при работе механизма. Этот способ не требует знания конструктивных параметров редуктора (количества зубьев или диаметров шкивов), но нуждается в точном контроле времени измерений.

Соблюдайте условия: механизм должен работать в штатном режиме без проскальзывания элементов передачи. Для замеров применяйте тахометр, энкодер или счетчик оборотов. Фиксируйте данные одновременно для обоих валов с синхронизированным запуском измерений.

Формула и порядок расчета

Передаточное отношение (i) определите по формуле:

i = n_input / n_output

где:

n_input – количество оборотов входного (ведущего) вала за выбранный интервал;

n_output – количество оборотов выходного (ведомого) вала за тот же интервал.

Практический пример

Параметр	Входной вал	Выходной вал
Количество оборотов (за 1 минуту)	300	60
Расчет	i = 300 ÷ 60 = 5

Ключевые требования к точности

Исключите проскальзывание ремней/цепей (при наличии)
Убедитесь в отсутствии холостого хода (люфтов) в зацеплениях
Выполните 3-5 замеров для исключения случайных погрешностей

Практическое измерение оборотов двигателя для расчетов

Точное определение передаточного отношения редуктора требует знания частоты вращения валов: входного (связанного с двигателем) и выходного (приводящего нагрузку). Непосредственно измерить передаточное отношение физически невозможно – его вычисляют по формуле на основе скоростей вращения: i = n_двиг / n_вых, где n_двиг – обороты двигателя (об/мин), n_вых – обороты выходного вала редуктора (об/мин). Поэтому корректное измерение входных оборотов двигателя (n_двиг) является фундаментом для достоверного расчета.

Для замера применяют специализированные приборы – тахометры. Популярны оптические (лазерные) и стробоскопические модели. На вал двигателя (или ведущий шкив/шестерню редуктора) крепят светоотражающую метку. Луч лазера или импульс стробоскопа направляют на метку, при синхронизации импульсов прибора с вращением вала на дисплее отображаются обороты. Точность обеспечивает:

Ключевые аспекты измерения

Стабильность режима: Двигатель должен работать на номинальной (или требуемой расчетной) нагрузке при установившемся режиме вращения несколько минут для стабилизации температуры и скорости.
Точное позиционирование: Метка должна быть четкой, а датчик тахометра направлен строго на траекторию её движения. Вибрации кожухов искажают измерения.
Учет проскальзывания: При измерении через ременную передачу прямо на вал двигателя (до редуктора) нужно учитывать возможное проскальзывание ремня, вносящее погрешность; предпочтительнее прямой замер на валу двигателя.

Альтернатива – цифровые тахометры с контактным наконечником (посаженным на торец вала) или индуктивные/магнитные датчики (считывающие импульсы от закрепленного магнита или зубьев шестерни).

Особый случай: В электроприводах часто используют показания встроенных в двигатель энкодеров или сигнал тахогенератора. Такие данные могут выводиться на частотный преобразователь или ПЛК контроллер и считаются наиболее точными при наличии эталонной настройки и отсутствии помех в линии.

Метод измерения	Принцип	Достоинства	Ограничения/Требования
Оптический (Лазерный) Тахометр	Регистрация отражения света от метки	Бесконтактный, универсальный (подходит к большинству двигателей)	Требует четкой метки, плохо работает при сильной загрязненности, высокой температуре или ярком свете.
Индуктивный/Магнитный Датчик	Улавливание магнитных импульсов от зуба шестерни или вращающегося магнита	Высокая точность, подходит для работающих в пыли/масле узлов.	Требует установки магнитной метки или наличия шестерни; контакт с валом.
Энкодер/Тахогенератор Двигателя	Выходной сигнал вращения ("A/B импульсы" или напряжение)	Наивысшая точность, возможность мониторинга в реальном времени.	Требует подключения к системе контроля/регистрации, только для двигателей с данной опцией.

Проводите минимум 3 последовательных замера для исключения случайных сбоев и сравнения результатов. Расхождение должно быть < 1-2% для приемлемой точности расчета передаточного отношения. Расчеты проводите только со средним арифметическим значением замеров оборотов двигателя и выходного вала.

Передаточное отношение через моменты сил

Закон сохранения энергии связывает моменты сил на входном и выходном валах. Для идеального редуктора (без потерь) входная мощность равна выходной: \(P_1 = P_2\), где \(P = M \cdot \omega\). Момент на выходе \(M_2\) и входе \(M_1\) связаны через угловые скорости \(\omega_2\) и \(\omega_1\), что позволяет вывести передаточное отношение.

В реальных условиях учитываются потери на трение, вязкость смазки и деформации зубьев. КПД редуктора (η) снижает выходной момент. Формулы для расчета модифицируются: передаточное отношение определяется как \(i = \frac{M_2}{M_1 \cdot \eta}\) при установившейся работе без учета инерционных сил.

Ключевые соотношения

Идеальный редуктор:
\(M_1 \cdot \omega_1 = M_2 \cdot \omega_2 \implies i = \frac{\omega_1}{\omega_2} = \frac{M_2}{M_1}\)
Реальный редуктор:
\(M_1 \cdot \omega_1 \cdot \eta = M_2 \cdot \omega_2 \implies i = \frac{M_2}{M_1 \cdot \eta}\)

Параметр	Входной вал	Выходной вал
Момент (M)	M₁ (Н·м)	M₂ (Н·м)
Угловая скорость (ω)	ω₁ (рад/с)	ω₂ (рад/с)
Поток мощности	M₁ · ω₁ · η	M₂ · ω₂

Примечания:

η всегда < 1 (0.85–0.98 для одной ступени)
Формулы действительны при постоянной скорости вращения (без ускорения масс)
Для повышающего редуктора соотношение инвертируется: \(i = \frac{M_1}{M_2 \cdot \eta}\)

Ошибки в расчетах: пропуск ступеней редуктора

Типичная ошибка при расчетах – неучёт одной из ступеней многоступенчатого редуктора, например, из-за схематичного изображения конструкции или отсутствия детального анализа кинематической цепи. Это приводит к некорректному определению общего передаточного отношения, которое рассчитывается как произведение передаточных чисел всех ступеней (\(u_{общ} = u_1 \times u_2 \times ... \times u_n\)).

Последствия такой ошибки критичны: некорректный расчет крутящего момента и частоты вращения на выходе вызывает перегрузку узлов или несоответствие техническим требованиям. Например, если пропустить ступень двухступенчатого редуктора с \(u_1=10\) и \(u_2=5\), вычисленное \(u_{общ}\) ошибочно составит 10 вместо 50, что занизит выходной момент на 80%, ускорит износ компонентов и сократит ресурс агрегата.

Как избежать ошибок

Тщательный анализ кинематической схемы: последовательно проверить каждое звено передачи от входного к выходному валу, включая планетарные и параллельные ветви.
Формализация расчетов: использовать алгоритм:
1. Определить количество ступеней редуктора.
2. Рассчитать \(u_i\) для каждой ступени отдельно.
3. Перемножить результаты: \(u_{общ} = u_1 \cdot u_2 \cdot ... \cdot u_n\).
Верфикация данных: сравнить полученное значение с паспортными характеристиками редуктора или провести практические замеры выходных параметров под нагрузкой.

Типичная ошибка при измерении диаметров шкивов

Основная ошибка – замер наружного (общего) диаметра шкива вместо расчётного диаметра, на котором располагается ремень. Наружный диаметр включает края ручья и не учитывает положение нейтрального слоя ремня, что искажает реальное передаточное отношение.

При измерении канавки шкива часто пропускают два ключевых нюанса: во-первых, глубину посадочного желоба, во-вторых – влияние типа ремня (клиновой, поликлиновой). Разница между наружным и расчётным диаметром достигает нескольких миллиметров, что при расчёте даёт погрешность до 5-8%.

Клиновые ремни работают на уровне условной линии, отстоящей от наружного края на 1/3 глубины канавки.
Поликлиновые ремни контактируют в самой широкой части ручья («по корду»).

Итог: используйте техническую документацию к шкиву или измеряйте расстояние от дна канавки до плоскости симметрии ремня. Если документация утеряна, примените таблицу поправок для профиля ремня.

Передаточное число ниже 1: когда это возможно

Передаточное число меньше единицы (i < 1) достигается при обратном соотношении: количество зубьев ведущей шестерни (Z1) превышает количество зубьев ведомой (Z2). Это происходит, когда оснастка преобразует высокий входной крутящий момент в повышенную скорость вращения на выходном валу при пропорциональном снижении усилия.

Основные сценарии использования редукторов с i < 1:

Повышение скорости вращения: Ветрогенераторы (передача от медленных лопастей к высокооборотному валу генератора), станки с ЧПУ (для шпинделей высокоскоростной обработки)
Ограничение крутящего момента: Конвейерные системы с защитой от перегрузок, манипуляторы с деликатным захватом
Компактность ведомого узла: Привода с малым межосевым расстоянием, где ведомая шестерня уменьшена для экономии места
Инвертирование направления: Многоступенчатые редукторы с реверсом потока мощности без применения паразитных шестерён

Расчет параметров для i < 1 демонстрирует обратно пропорциональное изменение характеристик:

Входная скорость, n1 (об/мин)	1000
Ведущая шестерня (Z1)	60 зубьев
Ведомая шестерня (Z2)	20 зубьев
i = Z2/Z1	20/60 = 0.33
Выходная скорость, n2 = n1 / i	1000 / 0.33 ≈ 3030 об/мин

Выходной крутящий момент при таком соотношении снижается пропорционально росту скорости: если на входе M1 = 300 Н·м, то на выходе M2 = M1 × i = 300 × 0.33 ≈ 100 Н·м (с учётом КПД). Такие редукторы требуют особого контроля вибраций и теплового режима из-за повышенных оборотов.

Проверка корректности расчета через КПД системы

Помимо расчета передаточного отношения (i) как отношения угловых скоростей или числа зубьев шестерен, его корректность можно верифицировать через коэффициент полезного действия (КПД, η) системы. Этот метод основан на сравнении теоретического усиления выходного момента, предсказанного передаточным отношением, с фактическим усилением, измеренным на практике. Фактический выходной момент (M_вых) всегда оказывается меньше, чем теоретический момент (M_теор = M_вх * i), из-за неизбежных потерь.

Основное соотношение связывает передаточное отношение, КПД и входной (M_вх)/выходной (M_вых) моменты: M_вых = M_вх * i * η. Зная входной момент, измеренный выходной момент и рассчитанное или паспортное передаточное отношение, можно вычислить фактический КПД установленного редуктора. Значительное отклонение этого расчетного КПД от типичных (паспортных) значений для данного типа редуктора однозначно указывает на ошибку в расчете передаточного отношения или в измерениях.

Источники потерь и практическая проверка

Потери, снижающие КПД и влияющие на связь между расчетным `i` и фактическим моментом, возникают из-за:

Трения в зацеплениях (гидродинамическое, контактное).
Трения в подшипниках качения или скольжения.
Вентиляционных потерь (перемешивание воздуха).
Потерь на перемешивание масла.
Гистерезиса в материалах.

Процедура проверки корректности `i` через КПД:

Измерьте входной момент на ведомом валу двигателя (M_вх).
Измерьте выходной момент на ведомом валу редуктора под нагрузкой (M_вых).
Используя формулу η = M_вых / (M_вх * i), рассчитайте фактический КПД системы.
Сравните полученное значение η с типичным (ожидаемым) КПД для данного типа редуктора.

Ключевой вывод: Если расчетный КПД значительно (на 10-20% и более) ниже или выше разумного диапазона для подобных редукторов (например, одноступенчатый цилиндрический: 0.97-0.98, червячный: 0.70-0.90, планетарный: 0.94-0.97), это вероятно указывает на ошибку в рассчитанном передаточном отношении `i`, в методике измерения моментов, либо на неисправность редуктора. Расчетное `i`, приводящее к реалистичному КПД в рабочем режиме, корректнее теоретического "кабинетного".

Применение онлайн-калькуляторов для верификации

Онлайн-калькуляторы передаточного отношения предоставляют оперативный способ проверки предварительных ручных расчётов, особенно при работе с многоступенчатыми редукторами или нестандартными схемами зацеплений. Алгоритмы таких инструментов автоматически учитывают межосевое расстояние, модуль зацепления и количество зубьев на всех колесах, минимизируя риск арифметических ошибок и пропущенных параметров.

Популярные платформы, включая GearCalc, 1728.org и специфические разделы инженерных порталов, позволяют вводить исходные данные в различных комбинациях – например, через диаметры делительных окружностей или характеристики электродвигателя и требуемой выходной скорости. Результаты сопровождаются визуализацией кинематической схемы и опциональным расчётом КПД системы.

Ключевые аспекты для валидации результатов

Проверка диапазонов: Калькуляторы с предупреждениями о выходе значений за пределы стандартных нормативов (например, передаточных чисел свыше 1:100 для одноступенчатых редукторов) повышают достоверность.
Сравнение нескольких ресурсов: Запуск идентичных данных в 2-3 независимых сервисах выявляет расхождения в алгоритмах и потенциальные ошибки.
Анализ промежуточных величин: Качественные инструменты отображают промежуточные параметры (угловые скорости ступеней, крутящие моменты на валах), позволяя отследить логику вычислений.

Важно учитывать ограничения: калькуляторы корректно работают только для типовых конструкций (цилиндрических, конических, червячных передач), тогда как планетарные схемы требуют ручной верификации. Результаты следует воспринимать как первичную проверку, обязательную к уточнению инженерными формулами для проектной документации.

Таблицы передаточных отношений для стандартных редукторов

Таблицы передаточных отношений служат справочным инструментом при проектировании редукторов, позволяя быстро определить стандартные значения без сложных расчетов. Они учитывают типовые конструктивные исполнения и нормированные параметры зубчатых передач, что упрощает подбор оборудования под конкретные задачи.

При использовании таблиц важно учитывать классификацию редукторов по типу передачи: для цилиндрических, конических, червячных и планетарных конструкций диапазоны существенно различаются. Данные сведены в удобную форму с указанием минимальных и максимальных значений, характерных для промышленных стандартов.

Примеры передаточных отношений по типам редукторов

Тип редуктора	Диапазон передаточных отношений	Особенности применения
Цилиндрический одноступенчатый	3:1 – 5:1	Компактность, высокий КПД (>95%)
Цилиндрический двухступенчатый	10:1 – 40:1	Баланс габаритов и нагрузки
Червячный одноступенчатый	5:1 – 100:1	Высокое снижение скорости, самоторможение
Коническо-цилиндрический	6:1 – 35:1	Изменение направления вращения валов
Планетарный одноступенчатый	3:1 – 12:1	Максимальная передаваемая мощность

Важные примечания:

Чем выше передаточное отношение – тем больше ступеней требуется
Значения для червячных редукторов могут достигать 300:1 при многоступенчатой компоновке

Определите тип механизма по таблице
Сопоставьте требуемую скорость вращения с диапазоном
Убедитесь в совпадении по крутящему моменту и монтажным размерам

Список источников

Точный расчет передаточного отношения редуктора требует опоры на авторитетные источники для исключения проектных ошибок. Используя проверенные материалы, инженер гарантирует корректную работу механизма и оптимальную производительность системы.

Приведенные ниже публикации содержат фундаментальные принципы кинематики, методики расчетов и практические примеры для определения передаточных отношений в редукторах. Они охватывают как базовые учебные материалы, так и специализированные нормативные документы.

Иванов М.Н. "Детали машин" – учебник с разделом по расчету зубчатых передач и многоступенчатых редукторов.
Решетов Д.Н. "Детали машин" – классическое пособие с формулами и схемами для кинематических расчетов.
Справочник конструктора-машиностроителя под редакцией Анурьева В.И. – разделы о редукторах и параметрах передач.
ГОСТ Р 50370-92 "Редукторы и мотор-редукторы. Термины и определения" – официальная терминология.
Курс лекций "Теория механизмов и машин" технических университетов – методики анализа кинематических схем.
Техническая документация производителей редукторов – каталоги SEW-Eurodrive, Bonfiglioli с примерами расчетов.
Научные статьи в журнале "Вестник машиностроения" по динамике передаточных механизмов.

Расчёт передаточного отношения редуктора - правильный метод

Суть передаточного отношения в механике

Ведущий и ведомый вал: ключевая терминология

Базовая формула для расчета передаточного числа

Связь количества зубьев шестерен с передаточным отношением

Особенности расчета для многоступенчатых редукторов

Расчет передаточного отношения для пар цилиндрических прямозубых шестерен

Практические аспекты расчета

Определение передаточного отношения по диаметрам шкивов

Расчет передаточного отношения

Особенности расчета для конических передач

Методика для червячных передач

Последовательность действий

Практический пример

Передаточное отношение цепной передачи на практике

Ключевые аспекты для практической реализации

Ременные передачи: тонкости вычислений

Учет проскальзывания

Планетарный редуктор: специфика расчета

Многоступенчатые редукторы: принципы вычисления

Ключевые аспекты расчёта

Перемножение передаточных чисел на разных ступенях

Пример расчёта для трёхступенчатого редуктора

Расчет общего передаточного отношения многоступенчатой системы

Ключевые аспекты расчета

Пример расчета для двухступенчатого редуктора

Влияние передаточного отношения на выходную скорость

Ключевые закономерности

Взаимосвязь передаточного числа и крутящего момента

Ключевые аспекты взаимного влияния

Пример расчета для двухступенчатого цилиндрического редуктора

Расчет по оборотам входного и выходного валов

Формула и порядок расчета

Практический пример

Ключевые требования к точности

Практическое измерение оборотов двигателя для расчетов

Ключевые аспекты измерения

Передаточное отношение через моменты сил

Ключевые соотношения

Ошибки в расчетах: пропуск ступеней редуктора

Как избежать ошибок

Типичная ошибка при измерении диаметров шкивов

Передаточное число ниже 1: когда это возможно

Проверка корректности расчета через КПД системы

Источники потерь и практическая проверка

Применение онлайн-калькуляторов для верификации

Ключевые аспекты для валидации результатов

Таблицы передаточных отношений для стандартных редукторов

Примеры передаточных отношений по типам редукторов

Список источников

Видео: котёл ГРИН и его редуктор. как правильно поставить?